Wystraszyły Cię kiedyś skomplikowane formuły matematyczne, które znaleźć można w wielu książkach o pokerze? Nie musisz się tym przejmować. Matematyka, której potrzebują wygrywający pokerzyści, wcale nie jest tak trudna do opanowania.
Ashley Adams to pokerzysta, trener i autor książek na temat strategii pokerowej. W swojej ostatniej książce, „Winning Poker in 30 Minutes a Day”, stara się pokazać, że nauka pokera może być prosta. Prosta, jak udowadnia Adams, jest też pokerowa matematyka. Jej podstawy przedstawił w artykule, z którym możesz zapoznać się poniźej.
1. Oddsy w przypadku drawów – metoda przez dwa i cztery
Gdy drawujesz do koloru, strita, fulla i tym podobnych, musisz wiedzieć, jakie jest prawdopodobieństwo tego, że skompletujesz swój układ. To kluczowy element opłacalnej gry w pokera. Masz do wyboru kilka sposobów. Możesz obliczyć oddsy w głowie. To wymaga pewnej umysłowej zręczności – a także szybkości, ponieważ będziesz musiał robić to w trakcie rozgrywania rozdania. Możesz zapamiętać procenty. To akurat nie jest takie trudne, ponieważ istnieje wiele tabelek, w których wymieniono najbardziej powszechne sytuacje. Większość poważnych graczy jest w stanie pamiętać o około 12 liczbach. Ale to nie wszystkie sytuacje, jakie mogą się czasami przydarzyć. Być może nie będziesz też na tyle pewny siebie, by łatwo przypomnieć sobie o procentach dla danej sytuacji.
Na szczęście istnieje bardzo dobra droga na skróty, dzięki której obliczysz potrzebne procenty. Nie jest to sposób w 100% dokładny dla każdej sytuacji, ale otrzymywane wartości są tak bliskie prawdziwym, że naprawdę warto go używać. Naucz się tej przedstawionej poniżej prostej formuły raz, a będziesz mógł wykorzystywać ją w każdej sytuacji.
Gdy drawujesz, powinieneś zacząć od obliczenia swoich „outów”. Outy to liczba kart, które są niewidoczne, a które skompletują Twój układ. Na przykład, jeśli zobaczyłeś już flopa i masz draw do koloru z dwiema kartami z ręki i dwiema z boardu, to wiesz, że pozostało jeszcze dziewięć kart, które skompletują Twój kolor (13 wszystkich kart w tym samym kolorze minus cztery, które zobaczyłeś). To dziewięć outów. Gdy masz open-ended draw do strita, to posiadasz osiem outów. Jeśli masz dwie pary i drawujesz do fulla, to pozostają Ci cztery outy. Wiesz już, o co chodzi?
Policz swoje outy. Aby obliczyć procentowe prawdopodobieństwo skompletowania układu, pomnóż swoje outy przez 2. W ten sposób dowiesz się, w ilu procentach przypadków skompletujesz swój układ na następnym streecie. Potem pomnóż przez 4, aby uzyskać procentowe prawdopodobieństwo skompletowania układu na riverze.
I tyle. Oto właśnie metoda przez 2 i 4.
Zróbmy szybki test. Jesteś na flopie. Trafiłeś gutshota. W ilu procentach przypadków skompletujesz strita na turnie? Na riverze? Uzyskałeś wyniki 8% i 16%? Jeśli nie, przeczytaj wszystko jeszcze raz. Iloma outami dysponowałeś ze swoim gutshotem? Tylko jeden rodzaj kart kompletuje Twój układ. Każdy rodzaj to cztery karty. Pomnóż tę liczbę przez 2, by uzyskać prawdopodobieństwo trafienia na turnie; pomnóż ją przez 4, by uzyskać prawdopodobieństwo trafienia na riverze. 4 outy razy 2 = 8%; 4 outy razy 4 = 16%. Proste, prawda?
2. Pot oddsy – jak dużo możesz wygrać, jeśli wygrasz
Gdy znasz już swoje oddsy, musisz dowiedzieć się, jak często wygrasz rozdanie po skompletowaniu układu. Powinieneś więc poznać swoje pot oddsy. Obliczysz je, porównując rozmiar puli z rozmiarem zakładu, który musisz sprawdzić, aby pozostać w rozdaniu i zobaczyć kolejną kartę. Na przykład, jeśli na turnie masz cztery karty do koloru, w puli jest 100$, a Twój przeciwnik betuje 100$, to musisz dołożyć 100$, aby wygrać pulę w wysokości 200$. Pot oddsy wynoszą więc 2 do 1. Proste, prawda? Weź po prostu wysokość puli, dodaj zakład rywala i podziel tę sumę przez rozmiar zakładu, który masz do sprawdzenia.
Oto kilka innych przykładów:
- Pula w wysokości 75$, bet za 50$. Całkowita pula wynosi 125$. Sprawdzenie kosztuje 50$. Podziel 125$ przez 50$, a otrzymasz pot oddsy 3 do 1.
- Jeśli w rozdaniu jest kilku przeciwników, jeden stawia 10$ do puli wynoszącej 30$, a trzech graczy sprawdza, to pula wynosi 70$ (30$ + 10$ + 10$ + 10$ + 10$). Za sprawdzenie zapłacisz 10$, więc Twoje pot oddsy to 7 do 1.
3. Czy Twoje pot oddsy uzasadniają drawowanie?
Zanim dowiesz się, czy powinieneś sprawdzać zakład z drawem, musisz zdecydować, czy ewentualna nagroda jest warta ryzyka. Upraszczając – musisz odpowiedzieć na pytanie: czy to jest dobre sprawdzenie? Nie trzeba bardzo się natrudzić, by znaleźć odpowiedź.
Po pierwsze, musisz ustalić oddsy dla swoich drawów. Wiesz już, jak najłatwiej to zrobić. Następnie powinieneś porównać pot oddsy do oddsów. Jeśli pot oddsy są większe od oddsów dla drawów, to sprawdzenie jest dobre. Jeżeli pot oddsy są mniejsze od oddsów dla drawów, to jest to złe sprawdzenie. Bardzo proste.
Oto łatwy przykład. Powiedzmy, że jesteś na turnie i masz 
, a board wygląda następująco: 
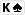
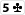. Posiadasz więc cztery karty do strita, ale jest to gutshot – KQJ9. Aby skompletować swój draw, potrzebujesz dziesiątki. Sądzisz, że Twój rywal ma najwyższą parę z najwyższym kickerem lub dwie pary. Wiesz, że jeśli skompletujesz strita, to wygrasz. Pula wynosi 1.000$, a rywal betuje za 500$. Czy powinieneś sprawdzić?
Opłacalny call wykonasz tylko wówczas, gdy Twoje pot oddsy będą wystarczające do uzasadnienia drawowania do dziesiątki. Więc najpierw musisz obliczyć, ile masz outów; potem użyć metody przez 2 i 4, by zobaczyć, jak często wygrasz. Są cztery dziesiątki, które skompletują Twój układ. Czyli masz cztery outy. Akcja dzieje się na turnie, więc pomnóż 4 przez 2. Otrzymasz 8, co daje Ci około 8% szans na skompletowanie układu. Oddsy na nietrafienie przez Ciebie układu wynoszą 12,5 do 1. Możesz wygrać 1.500$ za zainwestowanie 500$. To pot oddsy 3 do 1. Gdy porównasz pot oddsy 3 do 1 z oddsami dla drawu w wysokości 12,5 do 1, to oczywiste będzie, że pot oddsy są o wiele mniejsze – przez co sprawdzenie nie może być opłacalne. Cena, jaką musisz zapłacić, w tym przypadku nie usprawiedliwia drawowania.
Jak mogłeś się przekonać – pokerowa matematyka wcale nie jest taka trudna. Zapamiętaj opisane tutaj sposoby i używaj ich podczas sesji. Powodzenia!
Short Deck vs. No Limit Hold’em – główne różnice w strategii
