Konstantinos „Duncan” Palamourdas, profesor matematyki z UCLA, w artykule dla portalu Upswing Poker analizuje przykład tzw. czystego blefu, który wyrzucił z rozdania gracza z lepszą ręką.
Czy kiedykolwiek zastanawiałeś się, dlaczego czyste blefy działają?
Przez „czyste” rozumiemy tutaj sytuacje, w których stawiający zakład gracz posiada rękę bez żadnej wartości (także bez drawów), a gracz foldujący ma na przykład parę.
Przeanalizujmy przykładowe rozdanie z gry na żywo na stawkach 5$/10$ z efektywnymi stackami w wysokości 1.000$. Akcję otwiera siedząca na środkowej pozycji (MP) Alice, która przebija do 30$ z 
. Sprawdzić postanowił tylko gracz z big blinda – Bob – o którym Alice wie, że nie zwraca uwagi na pozycję, gra strategią loose-passive i lubi uczestniczyć w wielu rozdaniach.
Flop (pula: 65$):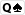 
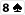
Bob czeka, a Alice betuje 40$, aby uzyskać trochę value ze swoją najwyższą parą. Bob niespodziewanie przebija do 200$.
Decyzja znów należy do Alice, która sądzi, że jest to bardzo niecharakterystyczne zagranie dla Boba. Gracz ten bardzo rzadko przebija bez silnej ręki – na przykład seta, overpary lub przynajmniej najwyższej pary z dobrym kickerem.
Uwadze Alice nie umknął oczywiście fakt, że Bob wykonał gigantyczne przebicie (pięć razy większe od zakładu Alice). Może to oznaczać, że Bob stara się ją wyrzucić z rozdania lub boi się kolejnej karty w kolorze pik. Alice nie widzi w zakresie Boba drawów, ponieważ z takimi rękami zdecydowałby się najczęściej na call.
Wygląda na to, że Bob ma spolaryzowany zakres – albo blefuje, albo gra z bardzo silną ręką. Alice uważa jednak, że jej przeciwnik raczej nie blefuje, więc wybiera opcję fold i wyrzuca swoją najwyższą parę.
Bob wyskakuje z krzesła i – choć dobrze wie o tym, że nie musi – pokazuje światu swoje karty. 
!
Miałem Brunsona! Nie mogłem się powstrzymać!
Alice od razu się uśmiechnęła i powiedziała: Very nice hand, sir! Wie ona oczywiście, że została właśnie wyblefowana z najlepszej ręki. Ale w jaki sposób mogła odgadnąć, że jej rywal zdecyduje się na blef z takimi kartami?
Prawda jest taka, że w tej sytuacji nie mogła tego odgadnąć. Bob zagrałby w dokładnie taki sam sposób z każdą silną ręką, która znajduje się w jego zakresie. Biorąc pod uwagę fakt, iż o wiele częściej będzie on miał tutaj wartościowe ręce, decyzja Alice była poprawna.
Warto dodać, że pokazania kart przez Boba było dla Alice bardzo użyteczne. Teraz wie, że T2 (przynajmniej w jednym kolorze) jest ręką, którą Bob lubi rozgrywać, więc doda ją do możliwego zakresu tego gracza.
Dlaczego blef Boba zadziałał tak dobrze przeciwko świetnie grającej Alice?
Odpowiedź brzmi: ponieważ jest on bardzo rzadki!
Innymi słowy, blef Boba jest wyjątkiem, a nie regułą. Gdyby Alice zauważyła, że Bob blefuje zbyt często, nigdy nie zdecydowałaby się na fold. Jedynym powodem, dla którego Alice spasowała, było to, że Bob nie blefuje wystarczająco często w podobnych sytuacjach. Zróbmy prosty rachunek, aby to potwierdzić, zakładając, iż przypuszczenia Alice są poprawne. Według niej Bob mógłby mieć następujące ręce: AQ, Q8s, 88, 55 lub T2s.
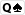
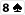
Przeanalizujmy także kombinacje tych rąk. Biorąc pod uwagę to, że Alice trzyma , a na boardzie widzimy , pozostałe kombinacje prezentują się następująco:
- AQ: 8 kombinacji
- Q8s: 2 kombinacje
- 88: 3 kombinacje
- 55: 3 kombinacje
- T2: 4 kombinacje
Alice przegrywa z 8+2+3+3=16 kombinacjami, podczas gdy wygrywa tylko z czterema. Daje to wynik 4 do 1 przeciwko niej. Pod oddsy były zbliżone do 2-1, więc oczywistym jest to, że znacznie częściej przegra. Matematyka podpowiada, że jej fold był poprawny!
Warto jeszcze zauważyć, że Alice nie musi wiedzieć, z jakimi kartami Bob blefuje. Musi jedynie obliczyć, jak często to robi. Więc dopóki Bob blefuje rzadziej niż z ośmioma kombinacjami, powinna ona foldować za każdym razem! Dokładnie tak, jak to zrobiła.
Patrząc głębiej
Powyższy stosunek (4 do 1) jest trochę niepoprawny, ponieważ nie bierze pod uwagę equity, jakie w rozdaniu ma Alice. Jej ręka ( ) ma około 25% equity przeciwko opisanemu wyżej zakresowi Boba. To oznacza, że jej stosunek przegranych wynosi tylko 3 do 1. To jednak również nie jest do końca poprawne obliczenie, ponieważ Bob nie zawsze pozwoli Alice na zobaczenie obu kart (z turna i rivera). Ogólnie rzecz biorąc, stosunek 4 do 1 jest więc w tej sytuacji dość dobrym szacunkiem.
Nawet jeśli Alice uważa, iż Bob gra w ten sposób z niektórymi ze swoich lepszych drawów, to jej decyzja o spasowania nie powinna się zmienić. Jest tak, dlatego że takie drawy mają olbrzymie equity przeciwko rękom z jedną parą, a czasami są nawet faworytami.
Na przykład, jeśli do zakresu Boba dodamy 
, 
, , 
, 
, 
, , 
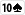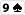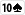
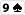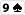
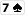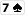
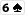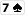
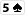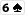
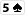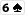
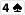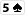
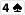, i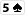 
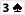, equity Alice wzrośnie jedynie do 35%, co oznacza, że w najlepszym wypadku będzie break even. A Bob nie zawsze przecież pozwoli jej zobaczyć kartę zarówno z turna, jak i rivera.
Ogólne tendencje
Podsumowując, Alice powinna pasować w podobnych sytuacjach, ponieważ Bob nie blefuje wystarczająco często. Pomimo tego, na co wskazywać mogą pokerowe programy telewizyjne, rzadko blefujący gracze nie są wyjątkami. Są oni raczej regułą w większości poker roomów, zwłaszcza na niskich stawkach.
Gracze zazwyczaj nie blefują tak często, jak powinni. W rezultacie ich zakłady są o wiele bardziej zbliżone do bycia „szczerymi” (np. ręce z value), niż „nieszczerymi” (np. blefy). Możemy to nazwać Zasadą Szczerości. Jej skrócona wersja wyglądałaby następująco:
Zasada Szczerości: Zazwyczaj, a także w dłuższym okresie czasu, poker to szczera gra.
Poprzez „szczera” chcemy tutaj powiedzieć, że jest bardziej szczera niż nieszczera w tym sensie, iż bety i przebicia są częściej wykonywane dla value, a nie dla blefu. Tę samą zasadę możemy też wyrazić w nieco inny sposób:
Zasada Szczerości: Pokerowa społeczność, jako całość, blefuje o wiele rzadziej niż powinna.
„Pokerowa społeczność” oznacza każdego człowieka, który gra w pokera. Zarówno graczy bez doświadczenia, jak i najlepszych pokerzystów na świecie.
Częstsze blefowanie dyktuje GTO (game theory optimal). Jest to bezpieczna strategia, która gwarantuje zysk dla używającego jej gracza – bez względu na to, jak grają jego przeciwnicy. Problem w tym, że nie wiemy, jak wygląda ta optymalna strategia, choć wiemy, iż istnieje, a wszystko za sprawą teoretycznej pracy wielkiego matematyka, Johna Nasha. Możemy jednak zbliżać się do tej taktyki „lokalnie”, poprzez skupianie się na konkretnych elementach gry, takich jak na przykład river. To, co zauważamy dzięki doświadczeniu, mówi nam, iż ludzie zazwyczaj blefują o wiele rzadziej niż powinni. Innymi słowy, zakresy graczy faworyzują value bety kosztem blefów, a różnica między tymi zagraniami jest większa w przypadku mniej doświadczonych pokerzystów.
