W jednym z ostatnich artykułów Ed Miller przedstawił Wam twierdzenie Bayesa, podstawową koncepcję probabilistyki. Zrozumienie tego co stara się przekazać Bayes pozwala w pokerze na podejmowanie wielu dobrych decyzji. Ostatnio pisaliśmy o tym jak ważne jest aby brać pod uwagę to jak często dany oponent blefuje. Jeśli ominęliście ten artykuł to warto do niego zajrzeć zanim przejdziecie dalej z lekturą.
Dzisiaj powiemy nieco więcej o czytaniu tego jak grają przeciwnicy i jak powinniśmy dostosować do nich swoją strategię. Nie raz na pewno będziecie musieli podejmować decyzje zanim oponent rozegra choćby jedną rękę. Twierdzenie Bayesa pomaga w takich sytuacjach i to bardzo.
Porozmawiajmy przez chwilę o betach kontynuacyjnych. Typowy gracz ze stawek $2-$5 sporo gra kontynuacyjnie. Jeśli popatrzymy przez chwilę na stół z tych stawek to zauważymy, że agresor preflop praktycznie zawsze robi c-bet, gdy sprawdza go jeden zawodnik. Bez znaczenia jest tu praktycznie pozycja, to czy gramy z blindów i jaki flop dane jest nam oglądać. Jeśli ktoś podbija preflop i zagrywa przeciwko jednemu przeciwnikowi to zazwyczaj c-bet jest pewny.
Każdy kto rozumie zasady no-limit hold’em wie, że wszystkie te rzeczy powinny wpływać na naszą decyzję o zagrywaniu. Zagrywamy przecież częściej, gdy mamy pozycję niż OOP. Częściej uderzamy w blindy niż w oponentów sprawdzających nas z innych pozycji i patrzymy na teksturę stołu.
W rezultacie są sytuacje, w których zagrywamy c-bet prawie zawsze. Są też takie, gdy lepiej zaczekać mimo, że przeciwnik tylko jeden i to my mamy inicjatywę PF.
Niby tak, z tym, że większość graczy $2-$5 nie rozumie tych niuansów. Zagrywają bardzo podobnie w zasadzie opierając się tylko o to jak ich karty wiążą się z tymi na stole. Jest też mniejsza grupa, która bierze wszystkie czynniki pod uwagę i można to wychwycić przy obserwacji.
Przyjrzyjmy się pewnemu rozdaniu. Gra $2-$5 ze stackiem 1000$. Jeden zawodnik limpuje, a przeciwnik, z którym nigdy nie grałeś podbija do 25$ dwa miejsca od buttona. Sprawdzasz z pozycji dealera, blindy odpuszczają, tak samo jak limper. W puli jest 62$ i gracie flop heads-up.
Flop to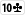 
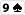
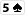. Twój przeciwnik stawia 35$.
Ogólnie rzecz biorąc nie jest to dobra sytuacja dla agresora. Został sprawdzony przez osobę nie z blinda i jest bez pozycji. Struktura flopu jest dodatkowo dynamiczna, co sprzyja graczowi z pozycją. Jeśli w grze HU są jakieś miejsca, gdy lepiej zaczekać z c-betem to to rozdanie jest idealnym tego przykładem.
Twój oponent jednakże zagrał. Zastanów się “czy ten bet to pomyłka?” Odpowiedź nie jest taka prosta. Może popełnił błąd, a może gra prawidłowo z asami na ręce. Nigdy z nim nie grałeś i nie znasz jego tendencji.
Załóżmy, że 80% graczy ze stawek $2-$5 źle c-betuje w takich sytuacjach. Pewnie wartość ta mogłaby być wyższa, ale weźmy 80%. Pozostałe 20% graczy $2-$5 c-betuje perfekcyjnie, więc tutaj ich bet byłby czymś podparty. (Oczywiście to bardzo ogólne założenie, nikt nie gra idealnie.)
Powiedzmy, że idealna wartość procentowa betu kontynuacyjnego to tutaj 30%. 20 dla rąk silnych, trafiających flop i 10 będących blefami dla równoważenia zasięgu do zagrywania.
Są więc cztery możliwości. „Słaby gracz” $2-$5 należy do tych 80%, którzy zagrywają źle. „Silny zawodnik” zagrał idealnie. „Słaba ręka” to jedna z 70 procent tych które nie powinny być betowane. „Silna ręka” to jedna z tych 30, które kontynuacyjnie zagrywać należy.
Silny gracz z silnymi kartami.- Silny gracz ze słabymi kartami.
- Słaby gracz z silnymi kartami.
- Słaby gracz ze słabymi kartami.
Mnożąc prawdopodobieństwo każdego zdarzenia możemy wyliczyć jak często nas ono spotka. Silny gracz, silna ręka to 0.2 x 0.3 = 0.06 czyli 6%. Silny gracz, słaba ręka to 0.2 x 0.7 = 0.14 czyli 14%.
Słaby gracz, silna ręka to 0.8 x 0.3 = 0.24 lub też 24%. Słaby gracz i słaba ręka to 0.8 x 0.7 = 0.56 = 56%.
Ważna uwaga – tylko trzy z tych danych procentowych równają się betowi. Dobry gracz ze słabymi kartami nie zagra. Nasze pierwotne pytanie brzmiało czy “ten bet to błąd?” Błędem jest tylko to kiedy słaby gracz zagrywa ze słabą ręką. Scenariusz 4 to szansa 56 procent, czyli więcej niż połowa. Odpowiedź na postawione na początku pytanie to nie 56 procent. Twierdzenie Bayesa znowu wchodzi do gry :)
Załóżmy, że rozdani to rozegramy 100 razy. W 14 przypadkach (14%), przeciwnik nie zagra, bo jest dobry i nic nie ma. To odrzucamy, bo nasz oponent zagrał. Z pozostałych 86%, 56 to błędne zagranie. Szansa na błąd wynosi wiec 56/86 = 0.651 czyli 65 procent.
Nigdy nie widziałeś tego zawodnika wcześniej i nie wiesz jak gra, ale możesz oszacować, że w 65% popełnił właśnie błąd.
Najlepszą obroną jest założenie, że oponent zrobił zły ruch. Możesz go od razu przebić lub sprawdzić z zamiarem oceny jego zachowania na kolejnych ulicach.
Zakładając, że przeciwnik się myli czasem sam popełnisz lekkomyślny błąd. Lepiej jednak czasem się sparzyć podejmując statystycznie dobre decyzje niż z góry zakładać, że człowiek po drugiej stronie stołu robi coś czego nikt nie potrafi – gra idealnie.
